Home
Syllabus
Schedule
Links
Homework
Homework
Suggested practice problems, not collected
A. Show that classical Möbius inversion is a special case of poset Möbius inversion.B. Let Cn be the poset consisting of all subsets of {±1, ..., ±n} which do not contain both +i and -i for any i.
Homework 12, due Apr 30 at 1:07pm
Please do the following problems from the textbook:Bona, p397: 24, 29, 37, 40, 41, 45
Poset products (as in Problem 29) are Definition 16.23 in Bona.
Homework 11, due Apr 23 at 1:07pm
Please do the following problems from the textbook:Bona, p366: 30a
And the following additional problems:
A. Let H be a d-uniform hypergraph, with m < 2d-1 edges, then the vertices may be 2-colored such that no edge is monochromatic (i.e., every edge contains both a red vertex and a blue vertex). Your proof should use the probabilistic method.
B. Show that if H is an intersecting hypergraph (not necessarily uniform) on n vertices, then |H| is at most 2n - 1.
C. Find an intersecting d-uniform hypergraph on 2d vertices, with (2d - 1 choose d - 1 edges), where the intersection over all hyperedges is empty. (That is, find a maximum intersecting family of d-sets other than {all d-sets containing a fixed vertex}.)
D. Let On be the graph consisting of n disjoint edges. Show for d <= n/2 that an intersecting family of independent sets of cardinality d has cardinality at most 2d * (n-1 choose d-1).
Hint: Pick a random q in Sn, a random i in [n], and n random coinflips, then proceed as in the EKR Theorem.
E.+ In the situation of D, prove that the set of all independent d-sets containing a fixed vertex v is a maximum intersecting family.
Homework 10, due Apr 16 at 1:07pm
Please do the following problems from the textbook: Bona, p260: 28
Bona, p300: 20, 22, 23, 30, 32
And the following additional problems:
A. Prove that R(n) <= R3(6, n).
Homework 9, due Apr 9 at 1:07pm
Please do the following problems from the textbook:Bona, p260: 8, 24, 25, 26, 27
And the following additional problems:
A. An alternate form of Hall's Marriage Theorem is stated as follows: let F = {S1, ..., Sm} be a family of subsets of [n]. A system of distinct representatives or SDR for F is a subset X={x1, ..., xk} of distinct elements of [n] such that for each i we have xi in Si.
Theorem (Hall's SDR Theorem) A family F = {S1, ..., Sm} of subsets of [n] has an SDR if and only if for every subset I of [k], we have | I | <= | Unioni in I Si |, i.e., 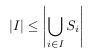 .
.
Give a short proof that Hall's Marriage Theorem implies Hall's SDR Theorem.
B. Give a short proof that Hall's SDR Theorem implies Hall's Marriage Theorem.
Homework 8, due Apr 2 at 1:07pm
Please do the following problems from the textbook: Bona, p200: 29, 38, 39, 42
Bona, p260: 5, 17
Note: Simple graph for us just means graph. The word 'simple' distinguished from graphs with "loops" and "multi-edges".
Homework 7, due Mar 24 at 1:07pm
Please do the following problems from the textbook:Bona, p168: 10, 29 (just find the explicit formula), 32, 35, 44a
Hint: It may be useful to consider F(-x) in one or more of the above problems.
Homework 6, due Mar 17 at 1:07pm
Please do the following problems from the textbook: Bona, p139: 27, 28+
Bona, p169: 23, 24, 42
And the following additional problems:
A. Honeybees: An egg laid by a queen honeybee grows into a female honeybee only if it is fertilized. Unfertilized eggs become male honeybees. Thus, female honeybees have two parents (one male and one female), while male honeybees have only one (female) parent.
How many grandparents does a queen honeybee have? Great-grandparents? nth-great-grandparents?
B. Prove that if X and Y are simplicial complexes, then the reduced Euler characteristic of their join X * Y is the negative of the product of the reduced Euler characteristics of X and Y.
C. For p139 #27, give a Moebius inversion proof, as well as an inclusion-exclusion proof.
Homework 5, due Mar 3 at 1:07pm
Please do the following problems from the textbook: Bona, p124: 45, 47,
Bona, p139: 16, 17, 18, 22, 24 (see also 9)
And the following additional problem:
A. Without using any deep results from class, show that the reduced Euler characteristic of the boundary of an n-gon is -1.
Homework 4, due Feb 24 at 1:07pm
Please do the following problems from the textbook:Bona, p122: 27, 29, 31, 38, 40
And the following additional problem:
A. Using Problem 38, find a new proof of Theorem 6.18.
Note: In Problem 29, the parity of a permutation is whether it is even or odd.
Homework 3, due Feb 17 at 1:07pm
Please do the following problems from the textbook: Bona, p103: 28 for k = 1, 29
Bona, p123: 11, 12, 33
And the following additional problem:
A. Let p be in Sn. Find an ordered basis {b1, ..., bn} of Rn such that (bi)Ap = bp(i), where Ap is as in problems 11 and 12, and the multiplication is of a row vector with Ap.
Homework 2, due Feb 10 at 1:07pm
Please do the following problems from the textbook: Bona, p77: 32, 50+, 52, 53
Bona, p102: 20, 21, 26, 27
Hint on p77 #50: Try to set up a bijection with a certain subclass of lattice paths from (0, 0) to (n, n). What does the non-intersecting property translate to?
Note: there is an error in the text for #51. The number of sequences should be Catalan, i.e., ( 2n choose n ) / (n + 1).
Homework 1, due Feb 3 at 1:07pm
Please do the following problems from the textbook: Bona, p51: 25, 27, 30, 33, 43, 48
Bona, p77: 33, 37
(Note that there is an error in p77 #37 in earlier printings of the book.)
And the following additional problem:
A. Explain why the last intersection of an NE lattice path ending at (k, n - k) with the reflection line y - n + k + 1 = x - k is a lattice point. (See class notes and solution to Exercise 4.19.)
Red text (like the plus sign in Problem A) reflect corrections made after the initial assignment.