In praise of simple models II

A common complaint of students in mathematics courses is that they are rarely shown how what they are learning is useful; they are asked to accept it on faith, and to wait till later to discover how it is used. Sadly, they often don’t, because many departments require calculus for their majors (because they think it makes them look serious) but never use it in their upper division courses, because the faculty is not comfortable using it in class. (I’m looking at you, Biology and Business!)

It is not a trivial problem to fix. Real applications take a lot of class time to develop, and so can only be added to the syllabus if other material is taken out. (Fake applications, like “ is a company’s profit function; maximize the profit” don’t help, since there is no indication of how one found this mysterious profit function in the first place). Personally, I favor taking some of the techniques of integration out of Calculus II. But so many different subjects use calculus (Engineering, Physics, Economics, in addition to our own majors) that it is hard to get consensus on removing anything from the syllabus.

To address this problem, I started teaching a course called “Applications of Mathematics” which is a one-credit add-on to our first semester calculus course. I start with problems where insight can come from simple models that do not use calculus, then, as the semester progresses, I introduce models that rely on topics covered in first semester calculus.
https://www.math.wustl.edu/wp/mccarthy/teaching/139Fall2019.html

Many of my examples are drawn from the wonderful book “The Pleasures of Counting” by Tom Korner. This a repository of “simple” models, carefully designed by great mathematicians, which give enormous insight. I put “simple” in quotes, because it requires great skill to winnow out the unneccessary complications that obscure the essence.

Here is one such example. During both the First and Second World War, Britain relied on imports from Canada and the United States. The transporting ships were attacked by submarines. Are convoys a good idea, and if so should there be many small ones, or a few big ones?

There are many factors to consider, as Korner describes. But the key insight is this. Suppose you have 12 destroyers (that can protect against submarines) and 40 merchant ships. If you have 4 convoys, each one gets 3 destroyers circling it. If you have one large convoy, its area is 4 times as large, but its perimeter only doubles. So you can achieve twice the density of destroyers in the perimeter, making it harder for submarines to get past the defensive cordon.

The fact that area goes up like the square of the radius, and the perimeter like the first power, make large convoys a good idea. (A similar theory would apply if merchant submarines were escorted by protective submarines in a three dimensional flotilla. The volume grows like the cube of the radius, the area of the surrounding shell like the square).

Here is another example, the SIR model of infectious diseases. This was developed by Kermack and McKendrick in 1927. It divides the population up into three groups:
, those who are Susceptible to the disease (having not had it);
, those who are currently Infectious;
and , those who are Recovered (and no longer infectious).

It assumes that the poulation mixes totally randomly, and that every time a susceptible person meets an infectious person there is some fixed probability that they will get infected. Infected people recover at a constant rate. There are three first order differential equations. We use ‘ to denote the rate of change (the derivative with respect to time).

   

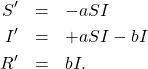
Here and are positive constants that depend on the virus. The first equation says that every time a susceptible person meets an infectious person, the probability of which is proportional to the product of those two populations, there is some chance that a person changes from susceptible to infected. The second one says that the number of infectious people goes up every time a susceptible person becomes infected, and goes down every time an infectious person recovers. The third one says that the number of recovered people goes up every time an infectious person converts.

The model just needs first semester calculus to understand, and it is easy to use. A critical number is the basic reproduction rate, called , which is
the average number of people each infectious person infects in turn. It is

   

where is the total population. If , the epidemic dies out. If it is greater than 1, eventually the whole population gets infected. The larger , the more rapidly the infection spreads.

The model is very simplistic – real world populations do not mix randomly, and the chance of an infection arising is not constant (wear masks!). But it is transparent, and easy to modify (for example, adding a fourth category of people who have been exposed, caught the virus, but are not yet infectious. This is the SEIR model). And the model has proved stunningly accurate at predicting the number of people to get COVID – see
https://e2a6b380-4bd5-43a8-b33f-68e981870108.usrfiles.com/ugd/e2a6b3_45c0e965321c4c9e86534595c8ac597f.pdf

Knowing how the model works has many advantages. If you want to decrease you have two choices – decrease (for example by wearing masks or social distancing) or increase (this is hard for COVID – it requires somehow decreasing the length of time people are infectious. But for other diseases, it shows the importance of treating asymptomatic yet infectious individuals.) When measured results start to deviate from the predicted ones, you know that one of the assumptions of the model is being violated. That in turn can be valuable information. If infections spike, for example, with no change in behavior, perhaps a more infectious variant has emerged.

Simple models are in many ways the opposite of the big data approach, which is premised on computers finding their own models to fit large data sets. I will discuss these “black box” models in a future post.