My work focuses on the connections between geometric measure theory, harmonic and complex analysis, and related fields such as elliptic partial differential equations. In addition to the brief descriptions below, all my preprints are available on
arXiv, and my CV is
here.
Preprints and Publications (listed chronologically)
- Improved Hölder continuity of quasiconformal maps, published in Ann. Acad. Sci. Fenn. Math. Quasiconformal maps have certain Hölder continuity properties, among other deep results in their regularity theory. These characteristics are related to some deep questions - for example, it is an open problem to find a (general) way of detecting when a solution to a Beltrami equation is bilipschitz. This is also related to the connectivity of the manifold of chord-arc domains. In this work, I gave a characterization of the Hölder continuity exponent based on a geometric term (via the isoperimetric inequality) and a structural term (depending on the Beltrami coefficient). This approach gives a way to characterize extremizers for Hölder continuity (quantitatively, they must be very close to pure radial stretches). These results generalize to a large class of elliptic equations in the plane.
- Geometric bounds for Favard length, published in Proc. Amer. Math. Soc. This work involves Favard length and Buffon needle problems in the plane, developing new techniques and estimates that apply to some classes of self-similar sets that arise naturally in fractal geometry. These can be used to give bounds for average projection lengths of sets. This gives an interesting notion of the size of a set (as well as a quantitative measure of rectifiability) that follows classical work of Marstrand and Besicovitch.
- Stretching and rotation sets of quasiconformal mappings, published in Ann. Acad. Sci. Fenn. Math. Quasiconformal maps have many useful geometric distortion properties; in this work I studied the size (in the sense of Hausdorff measure) of the sets where a given quasiconformal map can have prescribed stretching and rotation; these give quantitative measurements of the continuity of the modulus and argument, respectively. The analysis relies on a highly non-self-similar Cantor set construction (following ideas of my advisor Ignacio Uriarte-Tuero and the work of Lauri Hitruhin) and shows that the distortion sets can be extremely large (from many different perspectives - e.g. gauged Hausdorff measure and Riesz capacity).
- Commutators of Hilbert transforms along monomial curves (slides given at ORAM 2019); joint with Zihua Guo, Ji Li, and Brett Wick. Lp bounds for commutators are frequently used to characterize BMO spaces, going back to classical work of Coifman, Rochberg, and Weiss. For the Hilbert and Riesz transforms (among many other singular integral operators), commutators against a symbol b are bounded precisely when the symbol has bounded mean oscillation. In this work, we study what happens in the case that the operator is the Hilbert transform along a curve. This involves substantial new difficulties, because this operator is singular in a much different way than a typical Calderón-Zygmund operator. We give a partial characterization in terms of a curve-adapted BMO space related to BMO adapted to the parabolic grid.
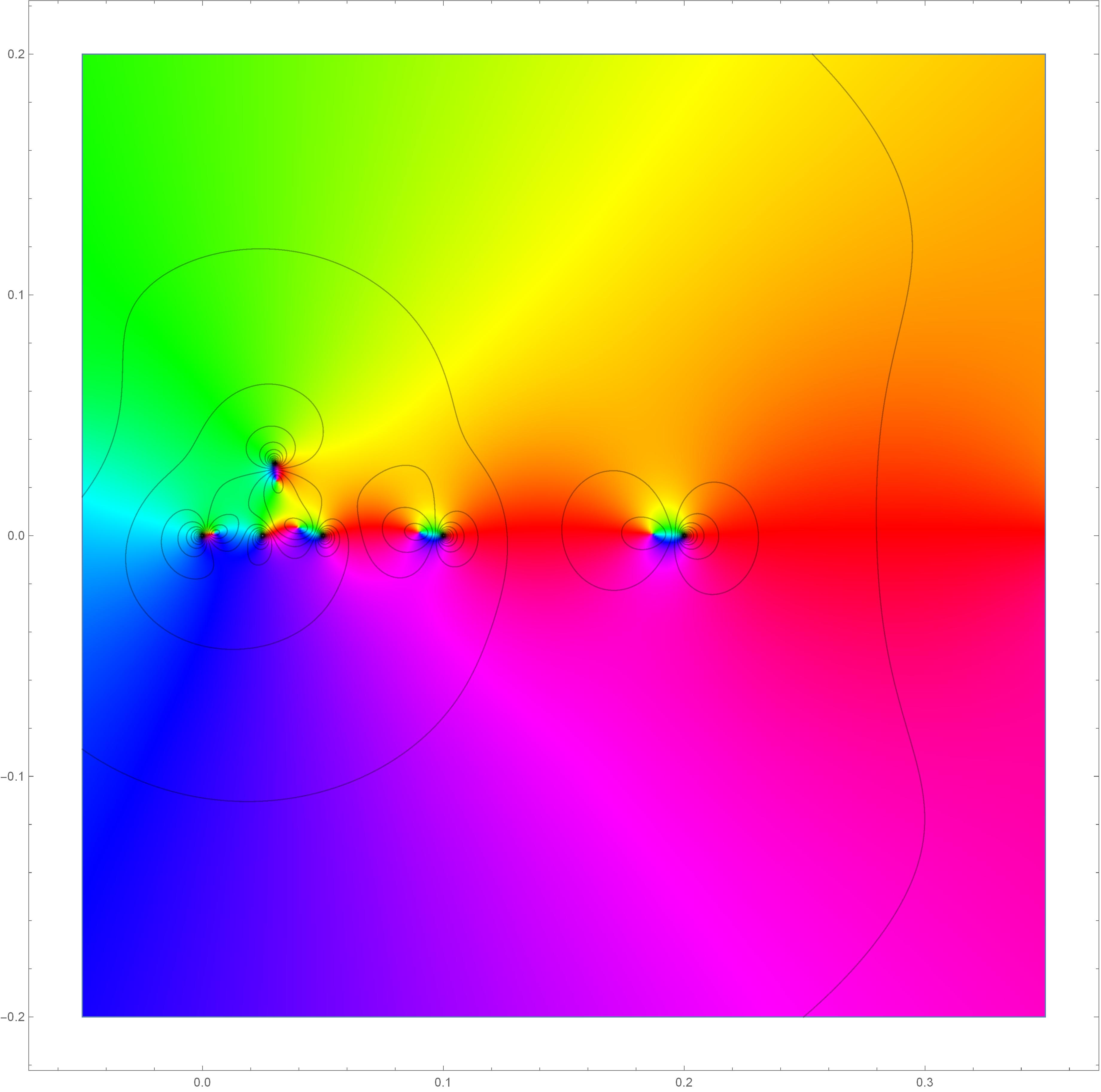Visualization of complex mapping with complicated stretching and rotation at six points in the plane.