When I day-dream about living in Heaven, I imagine playing rugby every Saturday afternoon. The teams will not need substitutes, because nobody will get injured. My team will win most of the time (as will everybody else’s – thanks to heavenly temporal anomalies). How often should my team win to maximize my happiness?
If we win all the time, there is no thrill about it. My gut instinct is that most happiness comes if we win 2/3 to 3/4 of the time. Let’s try and model it.
Assume the probability of winning is ![]() . Let
. Let ![]() be how much satisfaction I get from winning a particular game, knowing my win probability. The rarer winning is, the sweeter it is; so
be how much satisfaction I get from winning a particular game, knowing my win probability. The rarer winning is, the sweeter it is; so ![]() is a decreasing function of
is a decreasing function of ![]() . My overall long-term satisfaction is
. My overall long-term satisfaction is ![]() , the fraction of times I win times the satisfaction from each victory.
, the fraction of times I win times the satisfaction from each victory.
A first guess might be ![]() . After all, there is no thrill in winning if it is guaranteed. This would yield that
. After all, there is no thrill in winning if it is guaranteed. This would yield that ![]() , whose maximum occurs when
, whose maximum occurs when ![]() . But this seems too low. Observation suggests that people actually like winning even when the game is rigged in their favor — see how much more popular teams like Manchester United or the Yankees are than poorer teams that can’t afford to bid on all the best players. So perhaps
. But this seems too low. Observation suggests that people actually like winning even when the game is rigged in their favor — see how much more popular teams like Manchester United or the Yankees are than poorer teams that can’t afford to bid on all the best players. So perhaps ![]() looks like:
looks like:
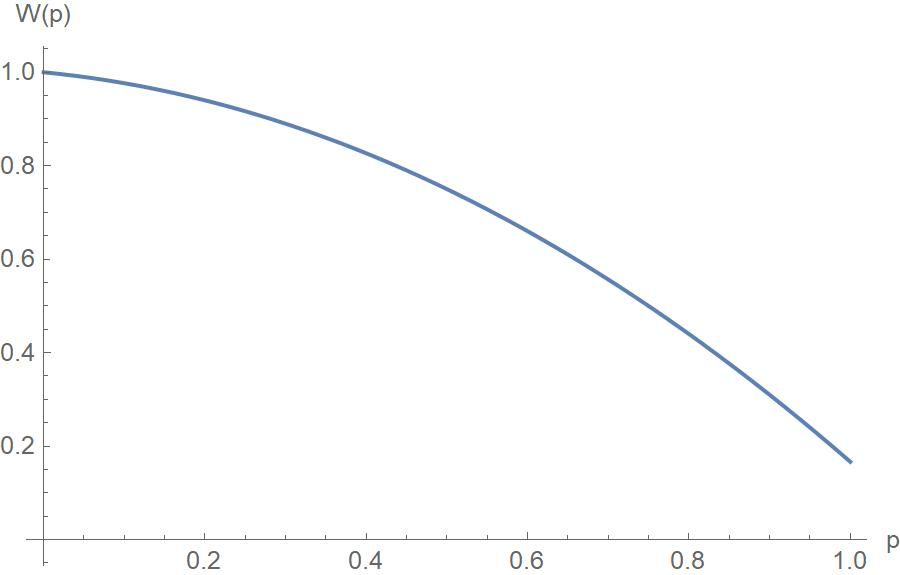
I chose ![]() , where the coefficients are just to get the general shape I want. My overall satisfaction then is
, where the coefficients are just to get the general shape I want. My overall satisfaction then is ![]() which has a maximum when the derivative of
which has a maximum when the derivative of ![]() is zero. Differentiating
is zero. Differentiating ![]() , which is a cubic polynomial, we get that
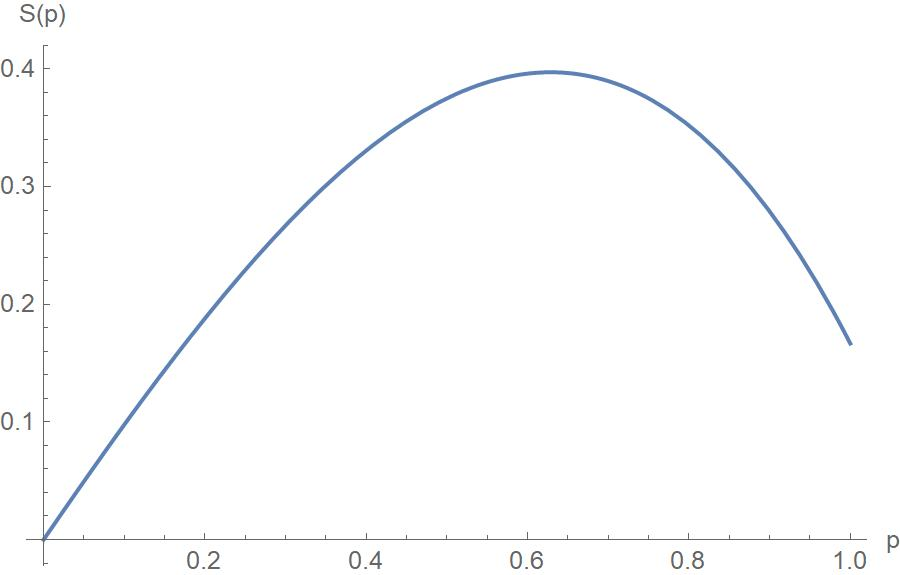
, which is a cubic polynomial, we get that ![]() . This vanishes at two points, which we can find from the quadratic formula. The one we want, the root where
. This vanishes at two points, which we can find from the quadratic formula. The one we want, the root where ![]() is between 0 and 1, occurs at 0.63.
is between 0 and 1, occurs at 0.63.
But wait a minute. If I derive pleasure winning a rigged game, maybe I deserve to play not in the Heavenly League, but the Infernal one. Using the formula for ![]() as above, Satan should ensure I lose every game to deprive me of all pleasure.
as above, Satan should ensure I lose every game to deprive me of all pleasure.
But Satan is smarter than that. I overlooked the pain that comes from losing. If I always lost, I would get numb. Instead, I have to win often enough that I have some hope (which is normally dashed — easy to arrange with infernal referees). By symmetry, let’s assume that the pain from losing is ![]() . Then my overall long-term satisfaction is
. Then my overall long-term satisfaction is
![]()
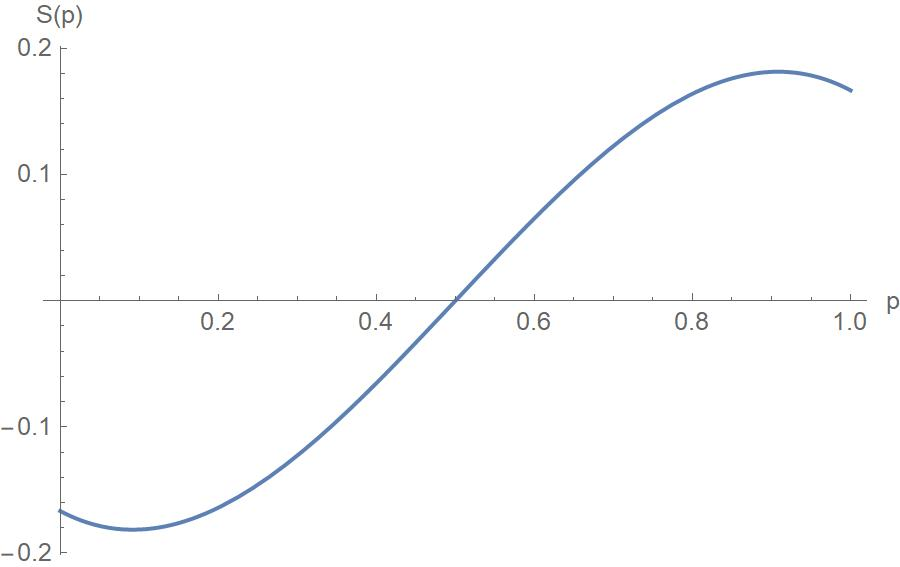
The roots of ![]() occur at .09 and .91. So in Hell my team wins 9% of its games (and they are all played in driving cold rain).
occur at .09 and .91. So in Hell my team wins 9% of its games (and they are all played in driving cold rain).
What happens if we change the coefficients of ![]() ? To get back to heaven, I will ensure
? To get back to heaven, I will ensure ![]() , so let’s assume that
, so let’s assume that
![]()
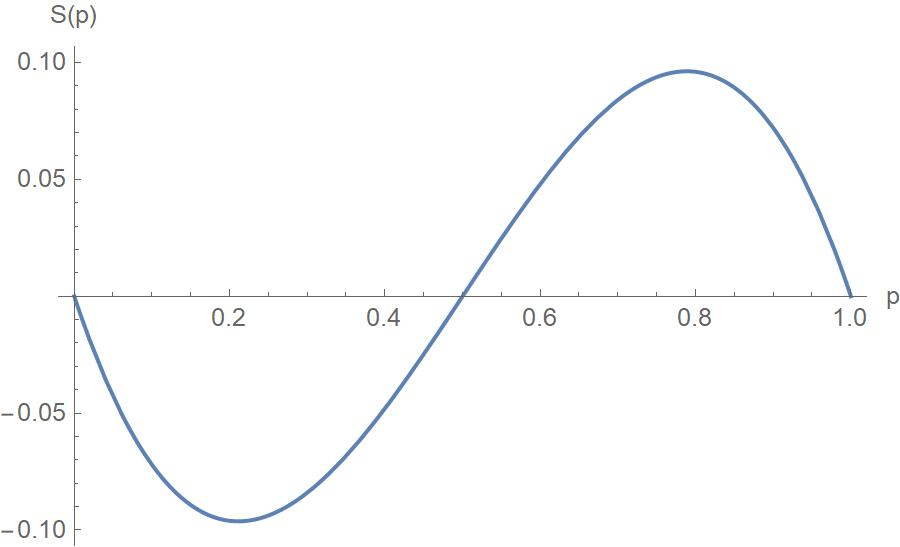
Surprisingly, changing ![]() does not change the shape of the curve. All it does is scale the curve in the vertical direction by a factor of
does not change the shape of the curve. All it does is scale the curve in the vertical direction by a factor of ![]() . More surprisingly, this is true even if
. More surprisingly, this is true even if ![]() for any
for any ![]() . So, the maximum happiness is always achieved at the same value. This is
. So, the maximum happiness is always achieved at the same value. This is
![]()
In Heaven, every team wins 78.9% of the time!
